If you’re responsible for maintaining motors, you may have sent units off to be reconditioned, only to see them demonstrate high vibration levels once they’re back on the foundation—and uncoupled to boot!
So now what? Your vibration technicians may be reporting high 1x vibration levels, which may point back to the repair facility. If they’ve documented their work, the repair facility will have data from the final test stand run indicating that vibration levels are well within satisfactory limits. Both answers can’t be correct. Or can they? Rather than waste time arguing with the repair shop, I suggest a more efficient approach—take more data. Chances are there’s critical information being overlooked and it can usually explain your problem. If your vibration technicians don’t know the answer, then they’re not asking the right questions—the kind that can be answered with more data or taking a closer look at the motor’s mounting and foundation.
Vibration data that includes a peak average coastdown spectrum will help isolate your problem. These readings will clearly identify any areas where the resulting high vibration is due to resonance (resonance is the condition where a natural frequency is close to—and thereby excited by—a forcing function, such as 1x operating speed due to residual imbalance). Impact data, when properly collected, can also identify natural frequencies. You have to be careful to impart sufficient energy in the frequency range of interest, using a soft tipped hammer with a large attached mass. If sleeve bearings are present, the rotor must be at a slow roll and not at rest. Failure to do this will couple a portion of the shaft stiffness into the end brackets, which will then yield erroneous information.
Let’s start with a little background on what we’re measuring. Induction rotor construction isn’t complicated: a solid steel shaft, thousands of thin laminations and either solid or cast bars connected to end rings. Modeling this rotor to identify its natural frequencies is easy, as a simplified 2D finite element program uses shaft lengths, diameters and material properties.
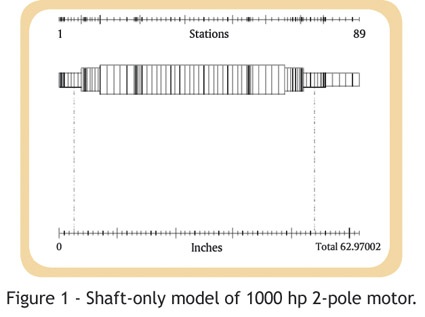
Figure 1 shows a model of a 1000 HP 2-pole motor (the laminations, bars and end rings are modeled but not shown). The 2D model requires a support stiffness that most closely approximates the structure supporting the motor—a motor bolted to a 2-inch sole plate, for example, embedded in grout that’s part of a 16-inch thick substrate. You, as the equipment operator and the primary construction contractor, are responsible for the equipment foundation. You must ensure that the rigid body modes don’t end up near major forcing functions, such as 1x and 2x running speed. In addition, the floor concrete must have been poured properly, with two feet of crushed stone underneath, for an equivalent support stiffness of approximately 400,000 lbs/inch. For whatever reason, your motor may not sit on a foundation this robust (most industrial applications using I-beam base construction have an equivalent support stiffness of approximately 100,000 lbs/inch, which is far from optimum).
There are other applications where the foundation has been designed specifically for lower stiffness, similar to the isolation pad testing. In these applications, the entire driver and driven units are isolated. This guarantees that the first two rigid body modes are well below operating speed. However, anything that the installation contractors do to compromise this isolation will cause excessive vibration for the same reason—the stiffness has now changed and the rigid body mode now coincides with operating speed. Other issues that can cause vibration include bottoming out of spring isolators or isolators that are incorrectly adjusted.
When we talk about lateral modes, remember that there are rigid body modes and bending modes. The motor design engineer can predict the bending modes, since they’re predicated on shaft stiffness and rotor mass. Most machinery has bending modes higher than twice operating speed. There are, however, machines that operate above the first and even the second bending mode (steam and gas turbines, for example). Some large motor frames operate above the first bending mode. You and the primary construction contractor responsible for the foundation have to ensure that the rigid body modes don’t end up near those major forcing functions, like 1x and 2x operating speed.
Figures 2 and 3 show the rigid body modes, with no bending in the shaft (you can see from the mode response that the bearing phases will be in phase for the first mode and out of phase for the second).
Figure 4 shows the first bending mode. You can see its frequency is 21,556 cpm or more than 3x operating speed for this 2-pole motor. You can also see that the mode shape curve crosses the center line, indicating true bending. The displacement at the bearings is out of phase for this mode.
The critical speed map results in Figure 5 are the key to understanding what’s happening with your reconditioned motor, now vibrating on its foundation. Note that a base stiffness somewhere between 50,000 lbs/inch and 100,000 lbs/inch is ideal for this motor. If your foundation is such that the equivalent support stiffness is close to 30,000 lbs/inch, then the second rigid body mode of the motor would be excited and the resulting vibration severe (this particular motor’s first rigid body mode is excited by an equivalent support stiffness near 200,000 lbs/inch; the red 1X running speed line coincides with the first rigid body mode curve). Equivalent support stiffness is the total stiffness in series from the bearing down to the earth. The weakest link in that stiffness chain largely determines the equivalent support stiffness.
Our example also illustrates that no matter what you change in a typical support stiffness setting, the first bending mode will be unchanged. The NEMA standard for testing motors on isolation pads is based on understanding the critical speed map. The isolation pads lower the equivalent support stiffness to the 1000-10,000 lbs/inch range, moving both rigid body modes well below running speed. The deflection of the isolation pad must be to specification—too soft or too hard and your motor could be in a rigid body mode on a test stand with very high vibration results. This often happens with large 2-pole sleeve bearing motors. The specification calls for approximately a 10% deflection of the isolation pads due to motor weight, which must be verified to prevent excessive vibration on the test stand.
You should also review a peak hold averaged spectrum to identify natural frequencies that might be close to operating speed. Figure 6 is an example of a coastdown on a large 2-pole motor in all three axes on both bearings. The motor was operating at 3585 rpm when the data averaging began and technicians then cut the power to the motor. The processor saved every amplitude data value during the coastdown until the process was stopped at approximately 20 Hertz, or 1200 RPM. Note that the amplitudes in three of the locations actually increase as the speed dips below 60 Hz. This identifies the residual imbalance exciting a natural frequency and driving it into resonance.
Figure 7 is an example taken on a large fan in the HVAC system of a 55-story building (20% of the building would be affected by the loss of this fan). The fan operated over a speed range as low as 200 rpm to 405 rpm. The peak average plot in Figure 7 captured the vibration over the entire operating range, revealing a resonance condition in the fan bearing pedestal nears 307.5 rpm. These fans were originally fixed-speed units. With the addition of variable frequency drives, it became apparent that there were speed ranges that had to be avoided. This unit now has a speed range that is blocked out to eliminate staying at the problem speed.
How do we measure support stiffness? The measurement requires a two-channel digital signal processor that has the capability to calculate the frequency response function (the ratio of the response motion to the input force excitation). The data is captured as impact data. Most digital signal processors will save all of the data necessary to give the results plotted in Figures 8 and 9.
The measurement in Figure 8 was taken on a large DC motor with a soft support system. The first cursor has been placed on the running speed of the motor (34 Hertz, or 2040 RPM). Figure 8 identifies a natural frequency response at 34 Hertz.
Figure 9 is the dynamic stiffness plot of the same impact test. Most dual channel digital signal processors calculate dynamic stiffness by taking the FRF, double integrating the response and then taking the reciprocal. Most FRF data is taken in accelerance (response acceleration in proportion to the impact energy). The reciprocal of acceleration is apparent stiffness. Remember, it’s important to keep the transducer units in order during this process. In this example, acceleration units of inch/sec/sec yields stiffness in lb/inch.
Note that the red trace (horizontal) dips at the running speed peak. This is because the stiffness is actually reduced at a natural frequency, thereby resulting in an increase in the vibration level. The response in the FRF will be a maximum peak and a valley will appear in the dynamic stiffness plot at the same frequency. The stiffness at this natural frequency is 9,536 lb/f (in/sec^2).
One more example: A customer recently sent a 2500 hp, 2-pole sleeve bearing induction motor to a shop for reconditioning. Following the reconditioning work, repair technicians ran the motor at full voltage on their test stand. The test stand foundation consisted of a 6 inch thick steel base imbedded in a sixteen inch concrete floor. The motor was set directly on the steel base with toe clamps grabbing the motor feet and securing them to pre-drilled holes in the steel base. The measured vibration levels on this motor were all well within satisfactory limits and bearing temperatures also stabilized well below stated limits.
The shop sent the motor back to the customer, but shortly thereafter, they received a call from the customer stating that vibration levels were not within tolerance (the motor was uncoupled at the time). Attempts to review a peak hold averaged plot or a properly performed impact spectrum from plant site personnel were unsuccessful. The motor was returned to the motor shop as defective.
Testing at the shop again revealed the motor was good. This time, the shop decided to send their field service technician to the customer along with the motor. After several hours on site, it became obvious what was wrong. The motor feet ran the entire length of the motor housing, front to back. The customer had only placed shims at the four corners. The field service tech shimmed the center of each leg and motor vibration dropped to satisfactory limits. Costly? Absolutely. Avoidable? Yes. A learning experience? Hopefully.
So the next time your reconditioned motor demonstrates more vibration than you like to see—and you’ve eliminated unbalance, misalignment, soft foot and every other possibility—take a look at your support stiffness. What’s changed? It could be something as simple as shorter shims instead of shims designed to support the entire motor foot. It could be corroded shims that don’t supply full surface support when restacked. Foundations don’t last forever. You may want to check for cracks in your concrete foundation or vibration in concrete pads, as this would signify that the fill below the concrete has washed away. The point is you need a complete evaluation of the operating environment, which means taking more data. If the motor had no problems when it came out, but does after reinstallation, it may not be the reconditioning work that’s at fault.
Remember—additional vibration data and inspection may be required to isolate the problem. The correct data can isolate the problems and help you resolve these issues before cracks appear in your relationship with the service provider.
Ron Brook is the Manager of Diagnostic Services at the Philadelphia Regional Service Center for Integrated Power Services. Ron is a Level 5 vibration expert with 34 years of vibration experience. His work covers vibration analysis, modal analysis and operating defection shapes, rotor dynamics modeling, vibration isolation and damping, finite element analysis and root cause failure analysis. Ron can be reached at 215-365-1500 or rwbrook@integratedps.com