Sin cuestionar este criterio globalmente aceptado, el objetivo de este trabajo es desarrollar un enfoque posible para resolver la cuestión: ¿Cuál es el Costo de Mantenimiento asociado al logro de un determinado objetivo de Factor de Disponibilidad, con una probabilidad de éxito definida?, en un complejo industrial.
Para comenzar con esto, vamos a homologar previamente algunos sencillos conceptos básicos de aplicación:
Factor de Disponibilidad (AF): porcentaje de tiempo en que el complejo está apto para producir (disponible) en relación al total del tiempo calendario evaluado.
Entonces, si:
UT: Tiempo de Indisponibilidad
T: Tiempo Total Evaluado
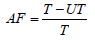
Tasa de Fallos (λ): Cantidad de Fallos contabilizados en un Tiempo definido. Es una medida histórica (hecho consumado). Está claro (y se da por descontado) que es conocido el concepto de fallo en relación a la función definida, con sus parámetros de aceptación, conforme a la filosofía del RCM. Se menciona asimismo que también consistentemente con los conceptos de RCM, la tasa de fallos puede ser genérica (cualquier fallo) u orientada a modos de fallo específicos, dependiendo la elección particular de las necesidades de aplicación. También se asume conocido que la medición se desarrolla típicamente sobre una población, lo que hace que la cantidad de fallos sea el verificado en el espacio muestral definido, y el tiempo computado el correspondiente al producto del tiempo calendario transcurrido multiplicado por el tamaño de la muestra.
Entonces, si:
FQ: Cantidad de Fallos
T: Tiempo Total Evaluado
Tiempo Medio entre Fallos (MTBF): inversa aritmética de la Tasa de Fallos. Es una medida histórica (hecho consumado).
Tiempo Medio de Reparación (MTTR): Promedio de los períodos de tiempo insumidos para las reparaciones, en un tiempo total de evaluación. Es una medida histórica (hecho consumado).
Entonces, si:
TTR: Tiempos de Reparación
T: Tiempo Total Evaluado
RQ: Cantidad de Reparaciones desarrolladas en T
A su vez, también se define:
Donde a μ se la conoce como Mantenibilidad, y que sería entonces la relación entre la cantidad de reparaciones desarrolladas en un período de tiempo total a evaluar, y la sumatoria de los tiempos insumidos en cada reparación, en ese período.
Disponibilidad (A): relación entre el MTBF y éste más el MTTR.
Confiabilidad (R): probabilidad matemática de que un activo ó conjunto de ellos alcancen el éxito en el desempeño de su función definida, en un período de tiempo determinado. Es una predicción estadística (a futuro).
Si asumimos un escenario de fallos aleatorios (como demuestran ser alrededor del 80% de los fallos una vez superada la etapa de fallos de infancia), lo que equivale estadísticamente a adoptar una distribución exponencial, y si:
λ: Tasa de Fallos Aleatorios
T: Tiempo Total Evaluado
Tiempo Medio No Productivo (MDT): Promedio de los períodos de tiempo de no producción, en un tiempo total de evaluación.
Entonces, si:
NPT: Tiempo de No Productivo
T: Tiempo Total Evaluado
NPPQ: Cantidad de Períodos de Tiempos No Productivos
A esta altura quedará claro que A (que es función de los MTBF y MTTR) se asocia a un enfoque de mantenimiento y AF (que es función del tiempo de producción) a uno productivo. Con esto en mente, vamos a comenzar entendiendo las sensibles diferencias entre A y AF, que pondrán en la superficie lo importante de no confundir conceptualmente uno con otro. Para evidenciarlo pondremos las cosas en el contexto de un ejemplo numérico:
Supongamos un escenario en el que, desde una perspectiva productiva, se propone como objetivo el logro de una cantidad máxima de 5 días no productivos, en 1 año calendario (estos 5 días se tomarán como la medida del MDT). Esto implica:
AF= 98,63%
Si ahora tomáramos este valor de AF como el de A (los forzamos iguales ⇒ A=98,63%), en base a una sencilla formulación algebraica que no detallaremos aquí (pero que se desprende de las expresiones básicas mostradas), y si asumimos un MTTR del 70% del MDT (por ejemplo), resulta que:
R (1 año)=23,5%
Lo cual significa que, si la Disponibilidad demostrable fuese de A=98,63%, asumiendo un MTTR del 70% del MDT, la probabilidad de alcanzar el éxito productivo planteado (AF=98,63%) en el año siguiente es de tan sólo 23,5%.
Supongamos ahora que el mismo escenario de propuesta de un objetivo de logro de una cantidad máxima de 5 días no productivos en 1 año calendario, se plantea alcanzarlo con una probabilidad de éxito de 95%. Si repetimos la premisa de un MTTR del 70% del MDT, resulta entonces que la A que debiésemos demostrar para satisfacer lo pedido es:
A=99,95%
Lo cual significa que, para lograr un AF de 98,63% (5 días no productivos en 1 año calendario) asumiendo un MTTR del 70% del MDT, con una probabilidad de éxito del 95%, se debe trabajar para obtener un valor de A de 99,95%.
A primera vista se podría pensar que no hay gran diferencia entre una A de 98,63% y otra de 99,95%. Veamos entonces qué significa en términos más evidentes, para lo cual desarrollaremos a su vez otro ejemplo numérico.
Supongamos que un modo de fallo determinado (orientamos en este ejemplo el concepto de fallo a modo de fallo), presenta un MTTR de 24 hs sobre un período de evaluación de 1 año calendario. En tal contexto, una A de 98,63% implicará un MTBF de 72 años. Si ahora proponemos una A de 99,95% para el mismo MTTR de 1 día, el MTBF requerido se eleva a 1999 años.
Otro camino ciertamente sería disminuir el MTTR. Ir de un A de 98,63% a otra de 99,95% manteniendo un MTBF de 72 años, implicaría reducir el MTTR de 1 día (el planteo original) a poco menos de 52 minutos.
No cabe duda que el ejemplo pone a las claras que, cuando hablamos de A y dado que usualmente MTBF >> MTTR, son necesario importantes incrementos de MTBF ó importantes decrementos de MTTR, para el logro de mínimos incrementos de A.
La cuestión inmediata ahora es, obviamente, cuáles son las acciones concretas de mantenimiento que soportan el logro de un objetivo de A.
Como ya vimos desde su expresión algebraica, A depende de MTBF y MTTR, ó lo que es lo mismo, de λ y de μ. Aumentar A implica aumentar el MTBF y disminuir el MTTR.
El control de la Tasa de Fallos λ se logra con un adecuado planteo de planes de mantenimiento preventivo y predictivo (PM/PdM), mientras que el control de μ dependerá del correcto desarrollo de los procedimientos de reparación y estrategias de repuestos.
No es objeto de este trabajo mostrar alternativas de desarrollo de planes de mantenimiento, procedimientos de reparación y estrategias de repuestos, pero sí se mencionará que para todo esto es extensamente aconsejable tomar en cuenta el uso de herramientas como RCM, FMEA, PMO, RCA, RBI, LOPA y RCS.
No se pierde de vista que obviar el desarrollo en detalle de lo mencionado en este último párrafo, no es una cuestión menor. Esto daría para pensar por ejemplo que si no se explica cómo los planes PM/PdM permiten controlar numéricamente λ, todo esto podría no pasar de ser un bonito planteo teórico. Para resolver esta duda razonable, sin entrar en profundos detalles, se mencionarán algunos conceptos que concurren a la sabia filosofía del RCM:
- Para diseñar un plan de mantenimiento, hay que entender previamente cuáles son los fallos que se quieren manejar.
- Los Modos de Fallo potenciales se deben proponer en base a la previa definición de las Funciones y los Fallos Funcionales, con atención a explícitos parámetros y criterios de aceptación.
- Un completo conjunto de Modos de Fallo para un activo determinado, se puede listar con el auxilio de FMEA. Por otro lado y esto si fuese posible y necesario, el mismo método de puntuación asociado al FMEA permitirá una selección previa de los Modos de Fallo más importantes.
- Las acciones de mantenimiento orientadas a resolver cada Modo de Fallo, deben observar un criterio de costo-efectividad.
- Las acciones predictivas y/o preventivas orientadas a resolver cada Modo de Fallo, deben tomar en cuenta el período P-F del mismo a los efectos de proponer una frecuencia de intervención, y su contenido conceptual tendrá como objetivo predecir y/o prevenir el fallo. Se destaca: la frecuencia de intervención está en función del período P-F y no de λ, que es una confusión bastante común.
Con todo esto en consideración, va resultando más claro que un plan de mantenimiento pensado en base a los fallos que se quieren manejar, con acciones específicas y frecuencias adecuadas, permitirá tomar control sobre λ, en términos de anticipación y prevención de la ocurrencia de la pérdida de una determinada función. Por supuesto, para que cualquier acción preventiva sea ejecutable sin afectar la función que se quiere conservar, la arquitectura constructiva del sistema que provee la función deberá ser adecuada. Donde no lo fuere y se lo encuentre costo-efectivamente conveniente, hay una oportunidad de mejora que deberá ser evaluada en función de su relación costo-beneficio.
Un capítulo aparte merece el mencionado LOPA (como una de la herramientas posibles), cuyo campo de aplicación alcanza específicamente a los sistemas de seguridad, y lo mismo para RBI en relación a los equipos estáticos.
Una vez desarrollado lo anterior, será necesario un conjunto de recursos de mantenimiento para su planificación, programación y ejecución.
Volviendo no obstante al primer hilo del planteo, si hablamos del logro de un objetivo de AF para una planta completa, ciertamente hablamos de lo mismo para A (en el marco de un valor de R como condición de borde). Y para ir desde un planteo de A para una planta completa a los planes PM/PdM y los procedimientos de reparación y estrategias de repuestos, hace falta comprender cómo la función de cada activo impacta sobre la función del complejo bajo análisis; y aquí es donde se propone el uso de Árboles de Fallos (FTA).
Para alimentar los FTA, se propone la utilización de RCM y/o FMEA y/o RBI para la identificación y parametrización de los Modos de Fallo, cada uno con sus Causas Iniciadoras y sus correspondientes MTBF y MTTR. La arquitectura lógica que interconecta las hipótesis de fallo hasta llegar a lo que se conoce como Evento Tope (en el lenguaje del FTA), permitirá el cálculo de la A y MTBF del mismo, que no es otra cosa que la función de la planta bajo estudio. Desde ya que estos FTA se podrán componer desde una desagregación previa en sistemas más pequeños, conforme lo permita el proceso involucrado y de acuerdo a la mejor conveniencia.
¿Y cómo se conecta esto con costos?. El desarrollo de los FTA (en base a RCM y/o FMEA y/o RBI), permitirá el diseño de los planes con el grado de detalle necesario. Tampoco es objeto de este trabajo, pero se menciona que todas las herramientas de confiabilidad mencionadas bien pueden armonizarse en el marco de un modelo de integración cooperativa, donde el RCA, el FMEA y el LOPA concurran a enriquecer las salidas de RCM, PMO y RBI. El RCS por su parte, cumple su función en la definición de los stocks de repuestos óptimos necesarios.
Es evidente a esta altura que, en términos de aplicación práctica, se habrán de seleccionar las herramientas que se juzguen balanceadamente valiosas en atención a la complejidad del problema a resolver. Lo que sí se resalta es que cualquiera sea el conjunto de técnicas de apoyo utilizadas, es importante el desarrollo del FTA para establecer con el grado de detalle necesario, la relación entre las actividades de mantenimiento y la A obtenible. Y es justamente esta definición detallada la que permite conectar A con los costos de mantenimiento asociados.
Para hacerlo más claro, los planes y procedimientos diseñados son los que deben permitir ganar control sobre la tasa de fallos λ y la mantenibilidad μ, en términos numéricos. Siendo estos dos parámetros los datos de entrada de las hipótesis de fallos en el marco del FTA cuyo cálculo final arrojará el valor de A de su Evento Tope, queda explícita la relación de cálculo entre los MTBF y MTTR de cada hipótesis de fallo y la A del sistema considerado.
Si encadenamos todos los conceptos expuestos, vemos que el costo del mantenimiento crece proporcionalmente con la demanda de AF. Siendo que a su vez el objetivo de AF se vincula a los presupuestos de producción y éstos con los objetivos de ganancia de la compañía vemos que, para un complejo dado, aumentar volúmenes de producción incrementa las ganancias sólo hasta el punto en que los costos de mantenimiento asociados al sostenimiento del AF requerido, comienzan a hacer disminuir la ganancia final. El conocimiento del álgebra de este balance, permite tomar decisiones de objetivos productivos consistentes con costos de mantenimiento (que desde ya, no son los únicos que concurren al costo final).
Este planteo integral no sólo permite dimensionar consistentemente un presupuesto económico de mantenimiento, sino que además le da un cuerpo estructurado, hilvanado y sólido a las estrategias del área, en base a los requerimientos productivos del complejo a mantener, en términos de AF y R.