Before we dismiss all these details so quickly, it is probably a good idea to understand the basics of the technology and its practical application. As with other automatic analysis and corrective recommendations from handheld instruments, a basic knowledge of what is going on behind the scenes and the physics of the measurements will instill a bit of confidence in arriving at the problem solution.
The first assumption that is made in most field balancing work is that we are dealing with a "rigid" rotor. A rotor is considered rigid if it shows no flexure throughout its operating speeds. A rigid rotor typically operates at a maximum running speed that is below 70% of what is called its first critical frequency, where it shows flexure in the middle of the shaft length. Next, we need to decide if we can balance the rotor in a single plane or whether we need to balance in two or more planes. Rigid rotors can be balanced in two planes, with two-plane balancing usually necessary when the length of the rotor exceeds three times its diameter. Most applications will utilize rolling-element bearings, where infinite stiffness is assumed in the support structure.
Before we begin our work on a machine, we should first establish our goals. We need to decide the balance criteria for the job and establish the maximum allowed amplitude for rotational vibration. There are several possible references, with the most common ones listed below. These are listed in no particular order, and depending on the customer (the requirements set forth by your facility or your client), one should be selected as your target.
- Manufacturer's recommended balance criteria
- ANSI S2.19-1989/ISO 1940 balance grades
- Machine average baseline + 1 sigma (standard deviation)
- MIL-STD 167; API 610
- Work experiences
Next, we need to be certain that we are really correcting a fundamental balancing issue. This is a very important step because we have to rule out any other related issues that might give us a false indication that we have an unbalance problem or could prevent us from improving the balance condition of the rotor. In the end, you don't want to try to "balance out" some other underlying vibration problem. This can prove to be a very frustrating and futile exercise. This is the time to perform further measurements and analyses to rule out other possible causes of a high 1X vibration level. Some of these potential problems are stated below:
- Dirt build-up,
- Rotating shaft instability,
- Looseness or excessive clearances,
- Bent shaft,
- Resonance,
- Cracked shaft,
- Structural or foundation looseness,
- Pulley/sheave eccentricity,
- Misalignment.
Our process is fairly straightforward. Unbalance can be represented by a spinning mass at a particular location outside the center of rotation. What we don't know when we start out with balancing is the magnitude of the mass and its location. If we did know, we could put an equal mass opposite the unbalance mass to cancel out its effects. The task of balancing a machine consists of finding the amount of unbalance mass and its location, and then affixing one or more correction masses at appropriate places to cancel the effect of the unbalance mass. The machine will need to be started and stopped several times throughout the process. At a minimum, you will need to perform the following five steps:
- Original Run,
- Trial (Calibration) Run,
- Correction Run,
- Trim Runs (if required),
- Final Run (for before and after assessment).
We start out with an initial reading of vibration on the rotor. Since there most certainly will be a residual unbalance condition contributing to vibration at the 1X turning speed, we need to assess its magnitude as compared to the overall level and other vibratory forces present. If the overall amplitude of vibration exceeds published industry standards for the class of machine and a 1X component exceeds 80% of the overall value, then an unbalance condition is most likely the root of the problem. However, as discussed earlier, a 1X high component also could be due to structural looseness and a number of other root causes. Phase and amplitude measurements in two or more radial locations will help to pinpoint unbalance issues. Amplitude values will be close and phase will be 90 degrees from vertical to horizontal, showing a true radial force.
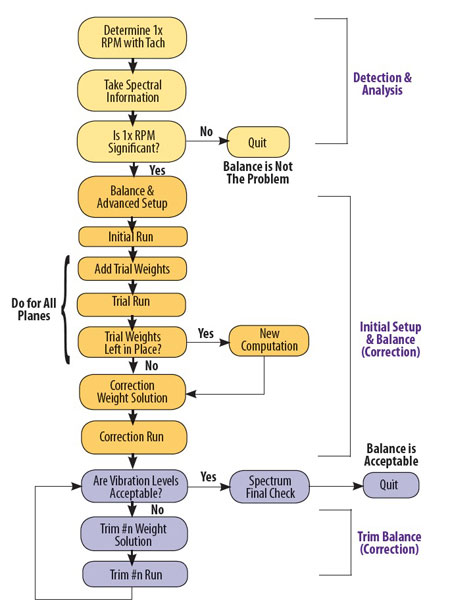
Figure 1: A flowchart for a typical field balancing procedure
Once we are convinced that unbalance is the machine's real problem and that it must be corrected, we need to look at the physical makeup of the machine and where we can make any weight modifications - both at the radius and the positions. We also need to look at where we place our transducer to see the most effects of the unbalance forces within the machine. For machines with the running shaft parallel to the floor, we typically see the most effect of movement in the horizontal plane, where there is a higher degree of freedom. The vertical movement is generally suppressed a bit by the gravity effect of the weight of the machine, the supporting structure and the holddown bolts.
Next, we need to consider safety factors for our work. We need to make certain electrical lock-outs exist during our steps for balancing and that we are running at safe speeds with safe trial (calibration) weights. Making sure of safety with lock-outs and appropriate notification and tagging, we need to estimate safe trial weights to be used. Sometimes this will come from field experience or a simple calculation. For normal running speeds between 1200 RPM and 3600 RPM, this is a simple estimate of trial weight in ounces given by 0.004*rotor weight (lbs.)/radius of weight (in.). It is important to note that the value of the trial weight is based on calculating a safe amount of weight to meet the so-called 30/30 rule (30% vibration change and/or a 30-degree angle shift.) To be more precise with actual running speed, the recommended trial weight (Wt) value in ounces is calculated as follows: Wt = 56,375 WR/(N2*r), where rotor weight (WR) is in pounds, speed (N) is in RPM and radius (r) is in inches.
One assumption for a rigid rotor is it can be balanced at any speed. A safe speed can be chosen below the actual running speed, all the way down to about 500 RPM. Unbalance forces are not linear with speed; they are proportional to the square of the running speed. Hence, an unbalanced rotor at one speed will have four times the unbalance force when the speed is doubled! Keep this factor in mind for safety.
After making the initial run and deciding to perform a balancing correction, the next step is to place a known trial (calibration) weight on the rotor at a known location and make another set of amplitude and phase readings. This step is used to determine the rotor characteristics, locate the heavy spot and calculate the corrective weight to minimize the original unbalance force. This weight location will always be 180 degrees opposite of the heavy spot on the rotor. It is important to note here that we are typically dealing with displacement as our measurement of vibration. We are not measuring the heavy spot, but we are seeing the high spot. However, for a rigid rotor running at 70% below critical, the high spot and the heavy spot are one and the same.
It is also important to note that we will see linearity in our placement of weight with a rigid rotor. As we place a weight at a known angle location, we will see a linear corresponding change in phase reading in the opposite direction. For example, if displacement phase is reading 165 degrees with a weight placement at 135 degrees, then moving that same weight to 180 degrees will result in a new phase reading at 120.
The trial weight (or calibration) step is where we determine the so-called "influence coefficients" of the rotor. The next step is to make some correction callouts. There are five critical parameters here that must be adhered to for effective field balancing:
- The exact same speed must be used on each run.
- The same radius must be used each time.
- Direction of placement must be consistent (against rotation-AR or with rotation-WR).
- Magnitude of readings must be stable within 5%.
- Phase readings must be stable within three to five degrees.
If any of these conditions show variation, then the system is not linear or there are outside influences, and any attempts to balance will be futile. Sometimes, this will appear to be a "chasing your tail" exercise, where things just don't seem to make any sense!
Once a correction is made, then the resulting vibration reading must be compared to an acceptable standard for the class of machine. It could be that the exact weight or position could not be met, so a trim run might be necessary. Each subsequent run should get to a convergence, i.e., where weight callouts are getting smaller and smaller and vibration levels are decreasing as well. If excessive weights are being called out and unbalance is getting worse with each run - the so-called "chasing your tail" scenario - it is time to stop and look for other machine conditions that are not associated with unbalance. Oftentimes, major outside influences like looseness, resonance and misalignment can impede the process.
So far, we have been dealing with a simple single-plane balance. Performing a procedure like this in two planes becomes an iterative process in determining the influence coefficients. It involves a couple of extra steps. First, we perform an initial run with two simultaneous unbalance readings - one in each plane. Next, we place a known trial weight at a known location in one plane and read its influence on the two planes. We remove that weight and place it (or a similar weight) at a known position in the second plane and read its influence on the two planes. At this point, we are done with calibrating and determining influence coefficients. The next steps follow recommended correction and trim weights in the two planes with weight callouts and locations. The same five rules stated earlier apply to step-by-step consistency and the stability of readings.
There are truly some elements of art and science involved in performing successful field balancing work. While microprocessor-based instruments with built-in software perform the required vector mathematics and geometry calculations, it really helps with the process to have a basic understanding of the tools and techniques involved. It also helps to benefit from others' field experiences in performing some tricks in arriving at an acceptable solution in a reasonable amount of time and number of trials.
Fundamental requirements for field balancing include three key elements: linear response in the system, accurate/repeatable test measurements and consistent weight placement. These might sound like simple assumptions, but any variations on these can produce significant problems in getting to an acceptable residual unbalance level on a machine component.