Se define “Diagnóstico proactivo e integrado” como un proceso que busca caracterizar el estado actual y predecir el comportamiento futuro de equipos, sistemas y/o procesos, mediante el análisis del historial de fallas, los datos de condición y datos técnicos, con la finalidad de identificar las acciones correctivas y proactivas que puedan efectivamente optimizar costos a través de la sistemática reducción de la ocurrencia de fallas y eventos no deseados, y minimizar en consecuencia, su impacto en el negocio medular. Adicionalmente, se destaca a la Ingeniería de Confiabilidad como el marco teórico-conceptual en el que conviven las metodologías y técnicas para lograr este fin; y adicionalmente se define Confiabilidad Operacional como un proceso de mejora continua, que incorpora, en forma sistemática, avanzadas herramientas de diagnóstico, metodologías basadas en confiabilidad y el uso de nuevas tecnologías, en la búsqueda de optimizar la planificación y la toma de decisiones. “Ingeniería de Confiabilidad; porque una de las mejores formas para agregar valor; es evitar que se destruya” [1]
1.- Modelos de Decisión en Mantenimiento
En años recientes, grandes corporaciones especialmente del sector de hidrocarburos y de la industria de procesos, han volcado su atención hacia el modelo de decisión “Costo Riesgo”, debido a que el mismo permite comparar el costo asociado a una acción de mantenimiento contra el nivel de reducción de riesgo o mejora en el desempeño debido a dicha acción.; en otras palabras, el modelo permite saber “cuanto obtengo por lo que gasto”.
El análisis “Costo-Riesgo” resulta particularmente útil para decidir en escenarios con intereses en conflicto, como el escenario “Operación – Mantenimiento”, en el cual el operador requiere que el equipo o proceso opere en forma continua para garantizar máxima producción, y simultáneamente, el mantenedor requiere que el proceso se detenga con cierta frecuencia para poder mantener y ganar confiabilidad en el mismo. El modelo Costo-Riesgo es el indicado para resolver el conflicto previamente mencionado, dado que permite determinar el nivel óptimo de riesgo y la cantidad adecuada de mantenimiento, para obtener el máximo beneficio o mínimo impacto en el negocio.[2]
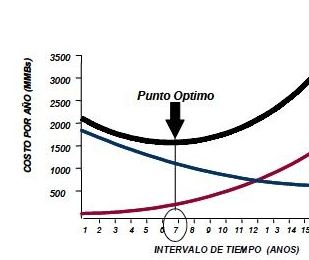
La figura 1 muestra gráficamente el modelo mencionado, y en el mismo pueden destacarse tres curvas que varían en el tiempo:
- La curva del nivel de riesgo (riesgo = probabilidad de falla x consecuencia), asociado a diferentes periodos de tiempo o frecuencias de mantenimiento
.- La curva de los costos de mantenimiento, en la cual se simulan los costos de diferentes frecuencias para la acción de mantenimiento propuesta
Para ampliar la imagen haga clic sobre ella, regrese utilizando su navegador.
La curva de impacto total, que resulta de la suma punto a punto de la curva de riesgos y la curva de los costos de mantenimiento. El “mínimo” de esta curva, representa la frecuencia para la cual la suma de los costos de la política de mantenimiento con el nivel de riesgo asociado a esta política son mínimos; es decir hay el “mínimo impacto posible en el negocio” Este mínimo esta ubicado sobre el valor que puede traducirse como el periodo o frecuencia óptima para la realización de la actividad de mantenimiento. Un desplazamiento hacia la derecha de este punto implicaría “asumir mucho riesgo” y un desplazamiento hacia la izquierda del mismo implicaría “gastar demasiado dinero”.
La dificultad para el uso del modelo, se centra en la estimación o modelaje de la curva del riesgo, ya que la misma requiere la estimación de la probabilidad de falla (y su variación con el tiempo), y las consecuencias En la próxima sección, se detallan las herramientas para lograr el correcto modelaje y estimación del riesgo.
2.- Riesgo, un indicador para el Diagnóstico Integrado
El riesgo R(t), base fundamental del modelo de decisión descrito en la sección anterior, es un término de naturaleza probabilística, que se define como “egresos o pérdidas probables consecuencia de la probable ocurrencia de un evento no deseado o falla”, y comúnmente se expresa en unidades monetarias, (Bs. o $).[1],[3]. Matemáticamente, el riesgo se calcula con la siguiente ecuación:
Riesgo(t)=Probabilidad de Falla(t) x Consecuencias
El análisis de la ecuación del riesgo, permite entender el poder de este indicador para el diagnóstico y la toma de decisiones, debido a que el mismo combina probabilidades o frecuencias de fallas con consecuencias, permitiendo la comparación de unidades como los equipos rotativos, que normalmente presentan alta frecuencia de fallas con bajas consecuencias, con equipos estáticos, que normalmente presentan patrones de baja frecuencia de fallas y alta consecuencia.
La figura 2, refleja gráficamente lo expresado en el párrafo anterior
Para ampliar la imagen haga clic sobre ella, regrese utilizando su navegador.
El riesgo, se comporta como una balanza, que permite pesar la influencia de ambas magnitudes (Probabilidad de Falla y Consecuencia de la Falla) en una decisión particular.
El mantenimiento moderno, sustentado en la Ingeniería de Confiabilidad, requiere de un cuidadoso proceso de diagnóstico de equipos y sistemas. El diagnóstico, basado en el “riesgo”, puede entenderse entonces como un proceso que busca caracterizar el estado actual y predecir el comportamiento futuro de equipos y sistemas.
Para el logro de un diagnóstico integrado, el riesgo debe calcularse usando toda la información disponible; es decir, debe incluir el análisis del historial de fallas, los datos de condición y datos técnicos. De esta forma, se podrán identificar las acciones correctivas y proactivas que puedan efectivamente optimizar costos y minimizar su impacto en el negocio medular.
La figura 3, muestra el proceso de “Diagnóstico Integrado”
Para ampliar la imagen haga clic sobre ella, regrese utilizando su navegador.
Entendiendo entonces que el “riesgo” es el indicador para un diagnóstico integrado, se analizará a continuación en detalle, el proceso para estimarlo.
3.- Estimación de Riesgo
Como se mencionó en el punto 2, el cálculo del riesgo, involucra la estimación de la Probabilidad de Fallas y/o la Confiabilidad, (Confiabilidad = 1 – Probabilidad de Fallas), y de las Consecuencias. La figura 4 muestra la descomposición del indicador “riesgo” en sus componentes fundamentales. En ella se muestra claramente que para calcular riesgo, deben establecerse dos (2) vías, una para el calculo de la confiabilidad y/o la probabilidad de fallas, en base a la historia de fallas o en base a la condición; y otra para el cálculo de las consecuencias.
Para ampliar la imagen haga clic sobre ella, regrese utilizando su navegador.
3.1.- Estimación de la Probabilidad de Fallas y/o la Confiabilidad.
Para la estimación de la confiabilidad o la probabilidad de fallas, existen dos métodos que dependen del tipo de data disponible; estos son:
- Estimación Basada en Datos de Condición, altamente recomendable para equipos estáticos, que presentan patrones de “baja frecuencia de fallas” y por ende no se tiene un “historial de fallas” que permita algún tipo de análisis estadístico.
- Estimación Basada en el Historial de Fallas: recomendable para equipos dinámicos, los cuales por su alta frecuencia de fallas, normalmente permiten el almacenamiento de un historial de fallas que hace posible el análisis estadístico.
3.1.1.- Estimación de Confiabilidad Basada en Condición
El análisis tradicional de confiabilidad, basado en el análisis estadístico del tiempo para la falla, ha sido exitosamente utilizado para mejorar el mantenimiento preventivo y traer los equipos y sistemas hasta los actuales niveles de desempeño. Sin embargo, buscando la mejora continua de sus procesos, en las tres últimas décadas, algunas industrias han hecho grandes esfuerzos en la recolección de data diferente a la data de falla, a través de programas de monitoreo de la condición (mantenimiento predictivo) con la finalidad de optimizar las frecuencias de mantenimiento de sus equipos y tomar acciones proactivas para evitar la ocurrencia de la falla.
La mencionada data de condición, ha sido usada principalmente en forma determinística, es decir, para hacer diagnósticos puntuales, debido a la falta de una adecuada metodología de análisis probabilística. En esta sección se establecen las bases conceptuales para el cálculo de confiabilidad y probabilidad de falla de equipos basado en la data de condición. La columna vertebral de este método es el análisis Carga-Resistencia [1].
a. Análisis Carga-Resistencia
El análisis Carga-Resistencia tiene como premisa el hecho de que las fallas son el resultado de una situación donde la carga aplicada excede la resistencia. Carga y Resistencia son usados en el sentido más amplio de la palabra; es decir, la carga pudiera ser la presión de operación, mientras la máxima presión de operación permisible sería la resistencia. Similar análisis se hace para cualquier otro parámetro relevante de la condición como vibración para equipos dinámicos, o reducción de espesor para el caso de equipos estáticos.
En todos los casos existirá un valor actual de la condición que se monitorea, el cual representará la carga, y un valor límite de la condición que representara la resistencia. Esta última normalmente esta regulada por normas y estándares de la ingeniería.
Contrario a la creencia general, en la mayoría de los casos ni la carga ni la resistencia son valores fijos, por el contrario, sus valores son estadísticamente distribuidos. Cada distribución tiene su valor medio, denotado por μY para la carga y μX para la resistencia y sus desviaciones estándar σY y σX respectivamente. Esto es ilustrado en la figura 5.
Cuando la distribución de la condición medida o monitoreada en el equipo tiene algún solape con la distribución de la condición límite o criterio de rechazo, en ese momento existe probabilidad de falla. Esta situación es mostrada en la figura 6.
La confiabilidad de un elemento bajo la aplicación de una carga es la probabilidad de que su resistencia exceda la carga. Dicha confiabilidad puede calcularse con la siguiente expresión: Confiabilidad = Probabilidad (Resistencia>Carga) [1],[5],[8],[9],[10]
Donde μY y μX son las medias de las distribuciones de la resistencia o criterio límite y el esfuerzo o condición monitoreada respectivamente, y σY y σX las respectivas desviaciones estándar.
NOTA: El operador “Φ”, indica que con el resultado obtenido de la ecuación entre paréntesis, debe buscarse el valor de probabilidad correspondiente en una tabla de la distribución normal
b. Estimación de la confiabilidad basada en la condición
Un parámetro de condición (PC) es cualquier variable física que revele información acerca de las características de desempeño de un equipo o componente. Un Parámetro Relevante de Condición (PRC) es un parámetro cuyo valor numérico caracteriza y cuantifica la condición de un equipo o componente en cualquier instante de su vida operativa.
Para que un PC sea un PRC, debe cumplir con los siguientes requisitos:
- Caracterizar la condición del equipo.
- Ajustar su valor continuamente durante su vida operativa.
- Describir numéricamente la condición del equipo o componente.
Un buen ejemplo de un PRC es el espesor de pared “E”, el cual es comúnmente usado en la industria petrolera para caracterizar el proceso de deterioro debido al fenómeno Erosión-Corrosión en tuberías en general y en algunos recipientes a presión. Otros PRC famosos en la industria del gas y del petróleo son:
- Nivel de Vibración (Equipos Dinámicos)
- Partículas Metálicas disueltas en el aceite (Equipos Dinámicos)
- Velocidad de Declinación (Pozos y Yacimientos)
- Presion Estática de Fondo (Yacimientos)
3.1.2 Predicción del Número de Fallas Basado en el Historial de Fallas
En este punto, se presenta la metodología y la plataforma matemática para predecir la disponibilidad en sistemas reparables, a través del tratamiento estadístico de su historial de fallas y reparaciones. En otras palabras, los equipos son caracterizados usando su distribución probabilística del “tiempo para fallar” y el “tiempo para reparar”.
Este tipo de análisis es particularmente valioso para equipos dinámicos, los cuales tienen una frecuencia de falla relativamente alta. Normalmente, la data de fallas y reparaciones está disponible.
Para equipos reparables existen cinco posibles estados en los que ellos pueden quedar, una vez reparados después de una falla:
- Tan bueno como nuevo
- Tan malo como antes de fallar.
- Mejor que antes de fallar pero peor que cuando estaba nuevo.
- Mejor que nuevo.
- Peor que antes de fallar.
Los modelos probabilísticos tradicionalmente usados en análisis de confiabilidad, se basan en los estados 1 y 2 (estados límites), sin tomar en cuenta los estados 3, 4 y 5 a pesar de que el estado 3 es más realista en la práctica. La razón para esto radica en la dificultad de desarrollar una solución matemática para modelar este estado.[3],[6]
Este trabajo muestra el modelo probabilístico desarrollado, el cual se denomina “Proceso Generalizado de Restauración” (PGR) [3],[6]. Este modelo elimina las limitaciones antes mencionadas porque toma en cuenta todos los posibles estados de un equipo después de una reparación. Esto da como resultado una nueva plataforma conceptual para análisis de confiabilidad en equipos reparables, la cual se ajusta en mayor grado a lo que sucede en la realidad, eliminando las desviaciones derivadas del uso de los análisis tradicionales, especialmente en cuanto a la predicción del número esperado de fallas y el tiempo para la próxima falla.
Formulación Matemática del PGR:
Las ecuaciones básicas del PGR tienen su base en distribuciones probabilísticas de Weibull condicionales [3], y son las siguientes:
A partir de estas ecuaciones básicas y de la data de fallas [(ti)=tiempos de operación entre fallas sucesivas] se calculan los parámetros “α”, “β” y “q”, cuyo significado es:
α : ”parámetro de escala”
β : ”parámetro de forma”
q : ”parámetro de efectividad de la reparación ”. Este parámetro puede interpretarse, según su valor, de la siguiente forma:
q = 0 tan bueno como nuevo
0 < q < 1 mejor que como estaba , pero peor que cuando era nuevo
q = 1 tan malo como estaba
q < 0 mejor que nuevo
q > 1 peor que como estaba
Para obtener los parámetros con este método existen dos alternativas[3] dependiendo del momento de ejecución del análisis.
a. Método de estimación de la Máxima Probabilidad de Ocurrencia (MPO), para aquellos casos en los cuales hay suficiente data disponible para el ciclo en análisis.
b. Teorema de Bayes para aquellos casos en los que no hay suficiente data disponible del ciclo en análisis.
Una vez estimados los parámetros de PGR es posible predecir el número esperado de fallas Λ(t), usando un proceso iterativo basado en simulación de Montecarlo [3],[6]. El diagrama de flujo para este proceso iterativo se muestra en la figura 7.
Los resultados de las estimaciones hechas con el PGR son mucho más certeros que las predicciones tradicionales. Como puede observarse en la figura 7.1, se generaron tres líneas de predicción basados en el 25% de los datos de fallas (puntos de falla encerrados con un cuadro) usando las tres teorías de predicción del numero de fallas:
- Proceso de Renovación Ordinario, basada en la asunción de un estado “tan bueno como nuevo” después de la reparación.
- Proceso No Homogéneo de Poisson, basada en la asunción de un estado “tan malo como estaba” después de la reparación.
- Proceso Generalizado de Restauración (PGR) que considera estados intermedios.
De las tres, solo la correspondiente al PGR coincide con gran precisión con las fallas que ocurrieron subsecuentemente.
4.- Estimación de Consecuencias.
En esta sección se presenta una metodología para estimar las consecuencias totales que resultan de la falla de un equipo y/o sistema. El modelo básico que soporta el trabajo aquí propuesto es el de “Impacto Total en el Negocio” desarrollado por John Woodhouse [2].
Modelo Propuesto:
El modelo divide las consecuencias asociadas con una falla particular en cuatro grandes categorías: Pérdidas de producción, costos de reparación, impacto ambiental e impacto en seguridad.
a. Pérdida de Producción:
En este paso, las pérdidas de producción debido a tiempo fuera de servicio son estimadas usando la siguiente ecuación: PERDIDA DE PRODUCCIÓN = PP * RF * TTR
Donde PP es el precio del producto ($/Unid), RF es la reducción de flujo (Unid/Hr) y TTR, el tiempo para reparar (Hrs). La variabilidad del costo del producto se incluye con la asunción de una distribución normal.
Reducción de flujo: La reducción puede ser total o parcial, dependiendo de otros factores tales como diseño, redundancias, cargas compartidas o stand by y/o severidad de la falla (critica o degradación). Para representar todos los posibles valores de esta reducción se definió una distribución normal.
Tiempo de reparación: En lo que respecta al tiempo de reparación, es su valor promedio (MTTR) el considerado para representar la distribución de esta variable.
b. Costos de reparación: La distribución de los costos de reparación debe incluir el espectro de todos los posibles costos, los cuales varían dependiendo de la severidad de la falla. Durante los ciclos de vida (tiempo entre overhauls), estos costos tienden hacia una distribución normal.
c. Impacto Ambiental e Impacto en Seguridad: Las distribuciones de estos impactos, en la mayoría de los casos, son difíciles de construir, pues no es fácil encontrar datos y fundamentalmente requieren ser construidas en base a la opinión de expertos.
5.- El Diagnóstico Integral en el Proceso de Confiabilidad
Como se ha estado describiendo en este trabajo, el diagnostico integral es un proceso que implica el uso de avanzadas técnicas de cálculo para predecir fallas y eventos no deseados e inferir sus consecuencias; es decir permite estimar el riesgo siguiendo el esquema de la figura 4 y también permite el uso de modelos de decisión como el Modelo Costo Riesgo explicado en el punto 1.
Hasta este punto, se han descrito brevemente las técnicas de la Ingeniería de Confiabilidad que permiten hacer estos cálculos.
El proceso conocido como “Confiabilidad Operacional”; es un enfoque metodológico donde el diagnóstico integrado se combina con otras metodologías tradicionales del área de confiabilidad, tales como: Análisis de Modos y Efectos de Fallas, Análisis Causa Raíz e Inspección Basada en Riesgo, entre otras; con la finalidad de:
- Inferir probabilísticamente todos los escenarios de producción factibles, a través de la predicción de los periodos de operación normal y de ocurrencia de eventos o escenarios no deseados, basados la configuración de los sistemas, la confiabilidad de sus componentes y la filosofía de mantenimiento
- Identificar acciones concretas para minimizar y/o mitigar la ocurrencia de estas fallas o eventos no deseados y llevar el riesgo a niveles tolerables
- Explorar las implicaciones económicas de cada escenario de riesgo posible y diseñar planes y estrategias óptimas para el manejo del negocio.
La figura 9, muestra el esquema de integración del Diagnostico Integrado con otras metodologías en el enfoque de Confiabilidad Operacional.
Conclusiones
1. La metodología de diagnóstico propuesta, basada en la estimación del riesgo, integra herramientas reconocidas de la Ingeniería de Confiabilidad, en una sola plataforma que permite:
- Realizar diagnósticos integrales sustentados en toda la información disponible de un equipo (data histórica, data de condición y data técnica).
- Hacer seguimiento al estatus de confiabilidad y riesgo de los equipos, subsistemas y sistemas con la finalidad de tomar las decisiones correctas en el momento adecuado.
- Comparar el costo asociado a una acción de mantenimiento contra el nivel de reducción de riesgo o mejora en el desempeño alcanzado debido a dicha acción.
2. El Proceso Generalizado de Restauración (PGR) usando simulación de Montecarlo para obtener el número esperado de fallas, representa una excelente herramienta para hacer predicciones de fallas en sistemas reparables. Los resultados obtenidos con esta herramienta son más reales que aquellos obtenidos con los métodos tradicionales basados en la asunciones “tan bueno como nuevo” y “tan malo como antes de fallar”. Este punto tiene gran potencial de aplicación en el área presupuestaria.
3. El método propuesto para el cálculo de confiabilidad basado en datos de monitoreo del deterioro o “datos de condición”, ofrece un método alternativo al tradicional método basado en la “historia de fallas”; que resulta particularmente útil para equipos y sistemas con tasas de falla muy bajas; tales como los equipos estáticos y provee además, una vía para incluir estas confiabildades en los modelos generales de plantas y sistemas; fortaleciendo los criterios para el diseño de políticas y estrategias de mantenimiento a las instalaciones.
Lecciones aprendidas
1. “Generalmente, no existen problemas complejos con soluciones sencillas”. El análisis de confiabilidad y riesgo en las instalaciones de procesos no es un problema sencillo, por ende, requiere de herramientas y metodologías de cálculo con complejidad acorde a la complejidad del problema. El uso de indicadores de confiabilidad sustentados en simplificaciones para dar mayor practicidad a su uso, con mucha frecuencia conduce a estimaciones y predicciones alejadas de la realidad, con el respectivo impacto en el negocio.
2. El proceso de diagnóstico de equipos, sistemas y/o procesos es una etapa de vital importancia en la mejora de la confiabilidad operacional, debido a que permite identificar las acciones proactivas que puedan efectivamente optimizar los costos y minimizar el impacto de los mismos en el negocio medular.
3. La ingeniería de Confiabilidad es una herramienta poderosísima para agregar valor a una empresa o proceso productivo; ya que una de las formas mas importantes de agregar valor, es evitar que se destruya.
REFERENCIAS
- Yañez, Medardo – Gómez de la Vega, Hernando, Valbuena Genebelin, Ingeniería de Confiabilidad y Análisis Probabilístico de Riesgo – ISBN 980-12-0116-9 - Junio 2003
- Woodhouse, John, “Managing Industrial Risk”, Chapman and Hall, Oxford, UK, 1993.
- Yañez, Medardo - Joglar, Fancisco - Modarres Mohammad, Generalized Renewal Process for analysis of Repairable Systems with limited failure experience – Reliability Engineering and System Safety Analysis Journal – ELSVIER – USA 2002
- Yanez, Medardo – Gómez de la Vega, Hernando, Valbuena Genebelin, Gerencia de la Incertidumbre – ISBN 980-12-0115-0 - Marzo 2003
- Roush M.; Webb W., “Applied Reliability Engineering”, vol I, The Center for Reliability Engineering, University of Maryland. College Park. 1999.
- Kritsov, Vasily. “A Monte Carlo Approach to Modeling and Estimation of the Generalized Renewal Process in Repairable System Reliability Analysis”. Dissertation For The Degree of Doctor of Philosophy, University of Maryland, 2000.
- Meeker, William Q.; Escobar Luis A., “Statistical Methods For Reliability Data”. Jhon Wiley & Sons, New York, 1998.Ahsmmed, M. “Probabilistic Estimation of Remaining Life of a Pipeline in the Presence of Active Corrosion Defects “International Journal of Pressure Vessels and Piping.” Vol. 75, 1998: 321-329.
- Ascher, H.;Feingold, H., “Repairable Systems Reliability: Modeling and Inference, Misconception and Their Causes”, Marcel Dekker, NY,1984ASM Metals Handbook, 13, 624, ASM Metals Park, Ohio, 1981.
- Ebeling, Charles E. “An Introduction To Reliability And Maintainability Engineering”. McGraw Hill. New York, 1997.
- Modarres, Mohammad; Kaminsky, Mark; Kritsov, Vasily. “Reliability Engineering And Risk Analysis”. Marcel Dekker, New York,1999.