Introducción a los Sistemas Lineales y No Lineales y su Relación con las Fallas en Maquinaria
Cuando se analizan los espectros de vibraciones de una máquina dentro del contexto de “linealidad” y “no-linealidad”, se tendrá un mejor entendimiento de porque los espectros se ven de cierta manera y esta apariencia relaciona con la “salud” de la máquina. Este artículo está escrito en un lenguaje simple para que pueda ser entendido aun por aquellos que no tengan bases técnicas.
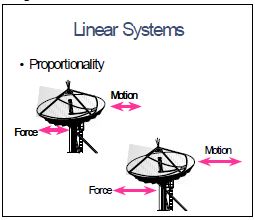
Sistema Lineal
Si se considera a un sistema lineal como una “caja negra”, se puede decir que lo que sale de la caja es directamente proporcional a lo entra en ella. Por coincidencia a esto es le llama “proporcionalidad” y se describe en la figura 1. Aquí podemos ver que el movimiento de salida esta directamente relacionado con la fuerza de entrada. Si la fuerza de entrada se incrementa, el movimiento resultante también se incrementa proporcionalmente.
La “superposición” es otra cualidad de un sistema lineal, como se muestra en la figura 2. “Superposición” significa que si tenemos 2 o más fuerzas de entrada, el movimiento de salida será proporcional a la suma de las fuerzas de entrada. En otras palabras, nada nuevo se crea. Si se agrega un grupo completo de fuerzas de entrada, el movimiento de salida continuará siendo directamente proporcional a la suma de esas fuerzas.
Sistemas No Lineales
Los sistemas no-lineales tampoco siguen la ley de “superposición”. Esto significa que la respuesta de salida no es proporcional a la suma de las fuerzas de entrada. En un sistema no lineal, las entradas se combinan entre sí y producen nuevos elementos en la salida que no estaban presentes en la entrada. (Figura 4)
Aquí hay otro ejemplo de sistemas lineales y no lineales que son fáciles de relatar. El ejemplo se muestra en las figuras 5 y 6. Cuando se enciende un sistema de sonido, llamado comúnmente “estéreo” a un volumen relativamente bajo, la música se escucha claramente. Cuando se sube el volumen suavemente, la música sale por la bocina más alta, pero el sonido sigue siendo bueno. Esta es una respuesta lineal.
Sin embargo nos encontramos en un punto donde si hacemos más ruidoso el estéreo, la música empieza a distorsionarse y nosotros empezaremos a escuchar nuevos sonidos que no estaban grabados en nuestro CD. Esta es una respuesta no-lineal. La clave otra vez, que para entender cuando algo es no lineal es que la salida contenga elementos que no estaban presentes en la entrada.
Linealidad y No-Linealidad en las Vibraciones
Ahora que hemos descrito los conceptos básicos de linealidad y nolinealidad, es tiempo de discutirlos en términos de las señales de vibración. Un simple sistema masa-resorte como se muestra en las figuras 7 y 8 será usado para esta discusión.
En la figura 7, tenemos un sistema ideal masa/resorte que se puede ser descrito por la ecuación F = KX, donde; “F” es la fuerza de entrada, “K” es la rigidez del resorte y “X” es el desplazamiento resultante del resorte. Este es un sistema lineal. Si le aplicamos en la entrada, una fuerza sinusoidal, el desplazamiento resultante también es sinusoidal y proporcional a la entrada.
En la Figura 8, la rigidez del resorte cambia ahora cuando está estirado y cuando está comprimido. Este es un sistema no lineal. Cuando le aplicamos en la entrada una fuerza sinusoidal, el desplazamiento resultante no es sinusoidal. Este, otra vez, obedece las reglas de los sistemas no-lineales, donde lo que se obtiene como resultado a la salida, es diferente a lo que entró.
Si recordamos nuestras reglas básicas de vibración y de la Transformada Rápida de Fourier (FFT), el desplazamiento de una onda sinusoidal de la figura 7 producirá un sólo pico en el espectro de vibración. La onda de desplazamiento de la figura 8 produce un pico en el espectro con armónicas (múltiples). Esto nos indica otro punto muy importante - las armónicas en este caso, son el resultado de las no-linealidades- .
Vibraciones de Máquina
Cuando nosotros vemos en el espectro de vibración de una máquina en el contexto de sistemas lineales y no-lineales, podemos hacer una declaración muy general; cuando las máquinas se deterioran y desarrollan fallas son menos lineales en modo de respuesta. También podemos decir que al tener muchas fallas en las máquinas, estas crean no-linealidad en su comportamiento. Por lo tanto, y también en términos muy generales, podemos esperar que el espectro obtenido en una máquina saludable, sea relativamente simple en comparación con el espectro de una máquina con fallas. Si nosotros consideramos a la soltura mecánica como un problema común en las máquinas, lo podemos demostrar de la siguiente manera: cuando la máquina no tenga holguras mecánicas y tenga buena salud, el espectro se verá como en la Figura 9.
En la figura 9, podemos ver el pico correspondiente al giro del eje principal (el más grande de la izquierda), y un par de armónicas de la velocidad del eje. La Figura 10, es de la misma máquina, pero cuando esta tiene un problema de soltura. Lo que podemos ver en la Figura 10, es que el número de armónicas correspondiente al giro del eje son mas numerosas y de mayor amplitud. Esto es muy similar al ejemplo de los dos sistemas de masa-resorte en los que, cuando el sistema masa-resorte era lineal, solo se produce un pico en el espectro, p.e. la salida vista como la entrada. Cuando el sistema masaresorte era no-lineal, la forma de la onda de salida no era sinusoidal y por lo tanto produce armónicas en el espectro.
Si nos vamos un paso atrás, podemos considerar que las fuerzas mecánicas de entrada en una máquina rotatoria simple vienen del eje de rotación. Si el eje rota perfectamente (p.e. no hay holgura) y la respuesta de la estructura de la máquina es perfectamente lineal entonces podemos esperar ver solo un pico en nuestro espectro correspondiente al rango del eje. En otras palabras, la salida debe verse como la entrada. Sin embargo las máquinas no son perfectas, y los ejes típicamente no rotan perfectamente alrededor de sus centros físicos de rotación y esto es por lo que esperamos ver algunas armónicas en el espectro de la máquina (como en la Figura 9). Sin embargo, conforme la máquina se vuelve más no-lineal, tal vez debido a la holgura, tendremos más armónicas con mayor amplitud (como en la Figura 10).
Note que si se observa el espectro con una escala de amplitud lineal, no se verán las armónicas contenidas en el espectro, ya que las armónicas son mucho más pequeñas en amplitud que los picos relacionados a la frecuencias del eje. Si se observan estos mismos datos, pero usando una escala de amplitud logarítmica, se verán más armónicas en la gráfica.
La Holgura, los Fracturas en la Base de la Máquina y los Tornillos de Sujeción Rotos pueden causa de no-linealidad en las máquinas, que puede resultar en la observación de múltiples armónicas en el espectro.
Bandas Laterales
La bandas laterals en el espectro son otro resultado de la no-linealidad. Las bandas laterals se producen por la amplitud modulada como se muestra en la Figura 11.
La forma de onda superior en la figura 11, es un ejemplo de forma de onda modulada. Lo que aquí tenemos es una onda que se repite con una frecuencia “X”, sin embargo, la amplitud de esta onda sube y baja a una frecuencia “Y” de la onda inferior del diagrama. La onda inferior solo se incluyó para demostrar la frecuencia a la cual la amplitud de la onda superior sube y baja.
Si usted desea visualizar esto en términos mecánicos, considere un grupo de engranes que no están centrados en su eje de rotación. Ahora, supongamos que el engrane no excéntrico tiene 32 dientes. En una revolución o giro del engrane no centrado, veremos 32 impactos producidos por los dientes. Relacione esto con la frecuencia indicada como “X”. Ya que este diente no esta centrado en su eje, la magnitud del impacto del diente sube y baja, según el engrane se mueve cerca o lejos del segundo engrane. Le tomará al engrane no centrado una revolución del nivel de impacto para ir de máximo a mínimo y regresar otra vez a máximo. Por lo que la frecuencia con la que el nivel de impacto cambia (o es modulada) es el rango de rotación del engrane no centrado. Relacione esto con la frecuencia mostrada “Y” en la Figura 12.
Si vemos el espectro de estos engranes (Figura 12), lo que veremos será un pico en la frecuencia “X” con un pico en ambos lados de “Y”. Dicho en otras palabras, veremos un pico en la frecuencia “X”, otro en “X+Y” y el tercero en “X-Y”. Los picos en “X+Y” y “X-Y” se llaman bandas laterales.
¿Entonces, por qué este sistema es no-lineal? Porque “X+Y” y “X-Y” no se encontraban en la señal de entrada pero aparecieron en la de salida. La única cosa en la entrada es “X” o el rango de impacto del diente. Estos impactos suben y bajan en amplitud en el rango “Y”, pero no es ciertamente “X+Y” o “X-Y” en la salida.
El engrane excéntrico también puede causar Frecuencia Modulada porque el radio efectivo del engrane descentrado cambia según se mueve cerca o lejos del otro engrane. Como el radio efectivo cambia, el rango de la velocidad de contacto del diente sube y luego baja repetidamente. La frecuencia modulada es similar a la amplitud modulada en que también resulta en banda lateral. En amplitud modulada, la amplitud del impacto sube y baja su nivel repetidamente, en frecuencia modulada, el rango de impacto es hace más rápido o lento repetidamente. En este ejemplo, ambas resultaran en el espectro en el mismo modelo.
Los elementos rodantes que usan los rodamientos, los defectos en los engranes, y los defectos en lsa barras del motor, todos estos elementos, producen bandas laterales. Los elementos rodantes de los rodamientos también crean tonos no-síncronos. Estos son nuevos picos que no son exactamente múltiplos (de armónicas) de la frecuencia de giro del eje.
La figura 13 muestra una máquina con un serio problema de rodamientos Compárelo con la figura 9 y vea que los picos que no están relacionados con la velocidad del eje (llamado 1X). Los dos picos marcados con círculos, son los tonos de los rodamientos y los picos con las flechas son bandas laterales. En términos del sistema lineal, podemos decir que este espectro representa una respuesta muy no lineal y sugiere que la máquina tiene fallas (que en realidad sí las tiene).
Para entender porque los elementos rodantes de los rodamientos crean tonos no síncronos y bandas laterales, debemos considerar el caso de una máquina horizontal con una falla en la pista interior del rodamiento. En el eje y con un giro de la pista interna del rodamiento, un cierto número de balines o bolas, impactarán la falla en la pista interior y producirán un pico en el espectro igual al número de impactos por revolución del eje. Este pico se llama, tono de rodamiento. El número de impactos nunca debe ser una cantidad múltiplo exacto a la frecuencia del eje. En otras palabras, debe ser 3.1 o 4.7 impactos por revolución, pero es muy raro si exactamente son 3 ó 5 impactos. Así, los picos no son múltiplos directos de la frecuencia del eje y por consiguiente “no síncronos”. El pico marcado con un círculo en la Figura 13, es un ejemplo de tono de rodamiento a 3.1x del rango del eje.
Considerando este ejemplo más allá, también podemos ver que el peso del eje puede causar el impacto contra la falla para hacerla de mayor en amplitud cuando la falla esta por debajo del eje. Como una falla en la pista interior rotativo en la parte superior del eje, el impacto será menor porque haymenos peso (carga) en la falla. En una revolución del eje la falla viajará alrededor 1 vez, en la zona de carga, fuera de la zona de carga y regresa a la zona de carga nuevamente. Por consiguiente la frecuencia del cambio de amplitud en este caso es igual a la frecuencia de giro del eje y este también coincide con el espacio de las bandas laterales alrededor del tono de rodamiento. Esos picos están marcados con flechas en la figura 13.
Un fenómeno similar ocurre si hay una falla en un balín o rodillo. Veremos un tono de rodamiento en una frecuencia igual al número de impactos de la falla que el balín hace con el aro del balero en una revolución del eje. Este pico también será no síncrono y se le llama tono de rodamiento. La falla en el balín o rodillo también viaja dentro o fuera de la zona de carga, sin embargo viaja en la frecuencia de la jaula, no en la frecuencia del eje. Por consiguiente, el espacio de las bandas laterales alrededor del tono del rodamiento, será igual a la frecuencias de de giro de la jaula, el cual usualmente es cercano a 0.3x del rango del eje.
Conclusión
El concepto de conducta lineal y no-lineal nos da otra forma de pensar a cerca del espectro de vibraciones y como es su apariencia relacionada con la falla en la máquina. Las máquinas saludables responden más linealmente que las máquinas con fallas, lo que quiere decir, que las máquinas que desarrollan fallas van a responder menos linealmente. Como van a ser menos lineales empezaremos a ver en el espectro más y grandes armónicas y o bandas laterales en nuestro espectro.
Debido a que no conocemos todos los detalles acerca del diseño de la máquina o como su espectro aparecerá cuando este saludable, es mejor a través del tiempo mantener información de tendencias. Esto quiere decir, ver más y grandes armónicas y nuevos picos que no había antes es una indicación de que la salud de la máquina se esta deteriorando.