This paper will cover several data analysis techniques that can be used to help understand the dynamics of asset failure. These methods are as follows:
- Pareto Analysis
- AMSAA Growth Analysis (MTBF Trending)
- Distribution Analysis (e.g. Weibull Analysis)
- System Reliability Modeling
Before we can discuss the use of these analytical tools we need to first address the data inputs. In order to use data analytics you must consider where your data is coming from and how valid it actually is. Primarily when using the analytics mentioned above, we will be using failure event data. This should bring up the question, what is a failure? Depending on who you ask you get a different answer. For instance, some may say that it is only a failure when there is a production loss. Others say the asset has to have a complete loss of function, therefore partial loss of function would not count. The fact is, for this type of data analysis we need to have a common definition of failure.
I would suggest using a definition that encompasses the following three levels of consequence:
- Complete Loss of Function
- Partial Loss of Function
- Potential Loss of Function
Let's explore some examples and reasoning for utilizing such a broad definition. Consider that you have a centrifugal pump that is designed to pump 200 gpm. If that pump had a component failure (e.g. bearing failed) and the pump could not pump at all that would certainly be considered a failure. Now suppose that for some reason that pump had a defect that only allowed the asset to pump 100 gpm. Is that pump meeting its intended function? I would argue that it was not. Lastly, suppose that that pump had a defect but did not cause a complete or partial loss of function (e.g. high vibration). When the decision is made to take the asset out of service to correct the problem, is that not a failure? Again, I would argue that it is indeed a failure of the asset to perform its intended function. If there were not a defect there would be no reason to take the asset out of service!
The point is that we need to know when assets and components do not perform their intended function. By having a very restrictive definition of failure you miss valuable data about he performance of individual assets.
Once the definition of a failure event is in place, you have to determine what data is important to fully describe the failure event. For instance, when a failure event occurs you need to know things like when the failure event occurred, what component failed, the failure mode, maintenance activity (e.g. replace, repair, inspect) and many others. Below is a table and description of critical information that is important to collect for any failure event.

Event ID - This is the unique identifier for each failure event.
CMMS ID - This is useful if you are using a CMMS system as the base data collection system for failure events.
Functional Location - The functional location is typically a "smart" ID that represents what function takes place at a given location. (Pump 01-G-0001 must move liquid X from point A to point B)
Functional Location Hierarchy - Functional hierarchy to roll up metrics at various levels
- Level 1
- Level 2
- Level 3
- Level ...
- Level n (System)
Equipment ID - The Equipment ID is usually a randomly generated ID that reflects the asset that is in service at the functional location. The reason for a separate Equipment ID and Functional Location is that assets can move from place to place and functional locations
Equipment Name - Name or description of Equipment for Identification purposes
Equipment Category (e.g. Rotating) - Indicates the category of equipment the work was performed on. Generally by discipline (Rotating, Fixed, Electrical, Instrument)
Equipment Class (e.g. Pump) - Indicates the class of equipment the work was performed on. Failure Codes can be dependent on this value
Equipment Type (e.g. Centrifugal) - Indicates the type of equipment the work was performed on. Failure Codes can be dependent on this value
Functional Loss - This indicates whether the equipment experienced a functional loss as part of this event. A functional loss can be defined as any of the following three types: (1) Complete Loss of Function, (2) Partial Loss of Function, (3) Potential Loss of Function
Functional Failure (ISO Failure Mode) - Basically the symptoms of a failure if one has occurred. Any physical asset is installed to fulfill a number of functions. The functional failure describes which function the asset no longer is able to fulfill.
Effect - The effect of the event on production, safety environmental, or quality
Maintainable Item - This is the actual component that was identified as causing the asset to lose it ability to serve. (e.g. bearing)
Condition - This indicates the type of damage found to the maintainable item. In some cases this also tends to indicate failure mechanism as well.
Cause - The general cause of the condition. This is not the root cause. It is recommended to use RCFA to assess root causes.
Maintenance Action - Corrective action performed to mitigate the damaged item
Narrative - Long text description of work and suggestions for improvements
Event Date - This is the date that the event was first observed and documented
Mechanically Unavailable Date/Time - This is the date/time that the equipment was actually taken out of service either due to a failure or the repair work.
Mechanically Available Date/Time - This is the date/time that the equipment was available for service after the repair work had been completed.
Mechanical Downtime - Difference between Mechanically Unavailability Date and Mechanically Available Date (in hours)
Maintenance Start Date/Time - This is the date/time that the equipment was actually being worked on by maintenance.
Maintenance End Date/Time - This is the date/time that the equipment was actually finished being worked on by maintenance.
Time to Repair - This is the total maintenance time to repair the equipment
Maintenance Cost - This is the total maintenance expenditure to rectify the failure. This could be company or contractor cost. This cost could be broken out into categories such as Material, Labor, Contractor, etc.
Production Cost - This is the amount of business loss associated with not having the assets in service. This cost includes Lost Opportunity, when an asset fails to perform its intended function and there is no spare asset or capability to make up the loss.
Once the work process is in place to collect the data, it is then possible to begin analyzing it. There are many ways to analyze data. From very simple methods like Pareto to more sophisticated methods like trending and distribution analysis. Do not mistake simple as not useful or effective. For instance, Pareto analysis is a very simple data analysis technique but it is extremely useful and valuable.
Pareto Analysis
The Pareto Principle or the 80/20 rule as it is sometimes referred was develop by an Italian Economist in the early 20th century. The principle was first based on income distribution. In other words, a very small portion of the population holds the majority of wealth. Since then, the principle has been applied in many different ways. In industry, we use it to track the defects or failures that occur and their overall importance. For instance, you will typically find that 20% or less of your assets represent 80% or more of the losses within a typical facility. This can be represented financially or by number of events.
Below is a sample Pareto Analysis:

This Pareto chart shows the top 30 centrifugal pump failures by the number of events each has experienced. Within each pump asset you can see the component or maintainable item that failed in the event.
The basic workflow for developing a Pareto analysis is as follows:
1. Determine your measures. For instance, what is your measurement criteria (e.g. Total maintenance cost, Total number of failures, Total lost profit opportunity, etc...)
2. Determine your x-axis dimensions. What do you actually want your measures plotted against? For example, a common Pareto would be to see the total cost of maintenance plotted against individual equipment types. You can see measures plotted against many different types of dimensions. Below is a list of common dimensions that can be used for a reliability Pareto analysis.
- Unit
- Equipment Category (e.g. Rotating)
- Equipment Group (e.g. Pump)
- Manufacturer
- Equipment Location
- Equipment ID
- Maintainable Item
- Failure Mode
- Cause Type
- Date (Year, Month)
- Failure Type (Total, Partial or Potential Loss)
3. Sort the data in descending order from highest importance to lowest importance
4. Plot the data in a histogram chart.
There are a number of effective tools to assist with Pareto analysis. It can be as simple as using a spreadsheet program like Microsoft Excel® or as sophisticated as using an OLAP (On-Line Analytical Processing) engine like the one that comes with Microsoft SQL Server®. Microsoft Excel® offers excellent data manipulation tools as well as a very sophisticated engine for performing Pivot Tables.

Sample Pivot Table in Microsoft Excel®

OLAP or On-Line Analytical Processing is a sophisticated tool to help analyst easily mine or drill down into their data. OLAP allows for the development of multi-dimensional cubes that allow analysts drill down from one x-axis dimension to the next lower level x-axis dimension. Below is an example of the drill down capability utilizing OLAP technology. The following series of graphs presents the failure cost of a refinery by production unit. By clicking on any of the units, the analyst is presented with the next level of detail. In this case, the asset ID's within the selected unit with the highest failure cost. By clicking on any of the asset ID's the analyst is then presented with the Asset subunit or failed item.

OLAP Graph - Refining Units

OLAP Graph - Equipment ID's within the Alkylation Distillation unit

OLAP Graph - Asset Subunit for PMP-4543, which is within the Alkylation Distillation unit
AMSAA Growth Analysis (MTBF Trending)
Army Materiel Systems Analysis Activity or AMSAA Growth Modeling is an analytical tool to trend Mean Time Between Failure or MTBF. This tool has multiple practical applications in the field.
The purpose of this tool is to plot MTBF data over time to determine if MTBF is increasing, decreasing or remaining constant. For example, assume that you have ten pumps in similar service. The plant underwent a new predictive maintenance strategy on these pumps 2 years ago. AMSAA can be used to trend the MTBF since the new strategy has taken place to determine the effectiveness of the new strategy. It can also be used in reverse as well. Perhaps the maintenance department wants to create a new predictive strategy on specific equipment and needs to demonstrate that MTBF has been trending down for a significant period of time. This helps make the case to create a new equipment strategy based on past MTBF performance.
The second main purpose for using AMSAA is to determine the validity of conducting a distribution analysis on specific failure modes. We will discuss distribution analysis later. In order to perform distribution analysis it is important to make sure that MTBF is not trending significantly higher or lower as time goes by. In order to use distribution analysis effectively, there has to be a constant failure rate to ensure that the data will provide a good "fit".
Let's take a look at an example dataset that might be used to perform AMSAA growth analysis.

The dataset is based on 24 failure events for two force draft fans in similar service. Note that this data has mixed failure modes which is acceptable with a growth analysis as opposed to a Weibull analysis where it would not give accurate results.

AMSAA Growth typically offers two parameters. The Beta and Lambda values. Beta is the slope of the growth plot. Similar to Weibull, but growth looks at cumulative time to event (failure) and not just individual times. Lambda is the Scale parameter. It equals the y-intercept of the growth plot at time t=1

The MTBF plot provides a visual representation of the MTBF as it has performed over a particular time period. It this case the MTBF for these two fans has trended positively over time indicating an improvement in overall reliability.
Weibull Distribution Analysis
Weibull distributions have been used effectively to help determine both the pattern of failure that a specific component experiences for a specified failure mode. In addition to identifying the failure pattern it also provides an accurate assessment of the characteristic life of the component for the same failure mode.
The failure pattern is a very important factor when determining what type of strategy to employ for a given component. The pattern of failure is based on the ‘reliability bathtub curve"

Time
Reliability Bathtub Curve
The three patterns represented by the "reliability bathtub curve" are:
- Early Failure or "Infant Mortality"
- Useful Life (Random Failure)
- Wear-Out Failure
Early failure indicates that the component has a higher likelihood of failure early in its life than later. In other words, it will likely fail close to the time it comes on line or into service. If it survives the initial startup period it will likely have a long life. This type of pattern is common for certain types of equipment like electronics. For instance, if you purchase a TV and it works for the first few weeks it will likely fail due to obsolesce rather than a specific failure. This pattern is also indicative of personnel avoidable problems like poor workmanship, incorrect startup procedures and other personnel avoidable issues. Many studies have shown than most failures occur in this pattern, which clearly shows that there is a lack of knowledge and skill in the maintenance and operation of our assets. When experiencing an infant mortality problem, it does not make sense to do planned or time based replacement maintenance, as it will only increase the chance of failure when the component comes back on-line.
Random failure patterns indicate that time is not a factor in our failures. For instance, a component may failure at 10 days, 100 days or 1000 days. The probability is the same for each of the time periods. Therefore planned replacement maintenance is not effective in this type of situation. Since time is not a factor in the failure there is no obvious time to do the planned replacement.
Wear out failure patterns indicate that the component has a useful life and that time is definitely a factor in the life of the component. For instance, piping corrosion at an oil refinery would typically have a wear out pattern. This simply means that some period of useful runtime takes place before the component begins to show signs of deterioration. Depending on the failure mechanism, the wear out rate can be very rapid or very slow. This is measured as the time from the first identifiable defect to the actual loss of the component.
Each of the failure patterns are represented by a parameter known in the literature as the Beta value (β). The beta value is simply a measure of the slope of the probability plot. Below is a table with Beta value interpretations.
General Rules for Beta:
| β < 1 | Indicates infant mortality |
| β = 1 | Indicates random failure |
| 1 < β < 4 | Indicates early wear-out failure |
| β > 4 | Indicates rapid wear-out failure |

"Reliability bathtub curve" with beta value interpretations
Weibull distributions also measure the characteristic life of a component at the point in time where 63.2% of the population in a give dataset has failed. This value is represented in time (e.g. hours, days, years, etc.). The parameter for this measurement is called the Eta (η)
Weibull Distribution Workflow
- Determine the asset(s) that you would like to analyze
- Determine the component/failure mode for that asset(s)
- Collect the dates when the failures have occurred
- Determine the TTF or Time to Failure values
- Determine the Eta and Beta values for the supplied TTF values
- Determine if the data provides a "good fit"
- Determine next steps (PM optimization, Failure Probability, Root Cause Analysis)
- Take action on results!
Step 1 - Determine the asset(s) that you would like to analyze
Weibull analysis can be used on multiple assets although it is important to make sure that the assets are similar in design and in the service they provide. For instance, you do not want to perform Weibull Analysis in a reciprocating pump in a water service and a centrifugal pump in hydrocarbon service. The failure modes and rates could be significantly different and consequently will provide inaccurate results in the analysis. So the general rule is to select a single asset or multiple assets if they are similar in design and service.
Step 2 - Determine the component/failure mode for that asset(s)
Once the asset is identified, you must isolate the component/failure mode because combining multiple components/failure modes will cause inaccurate results and many times will create a failure pattern of random due to the different failure rates of each component/failure mode.
Step 3 - Collect the dates when the failures have occurred
Determine the dates of each failure that has taken place. This is best described as the date that the asset was unavailable to perform its intended service. For instance, this is the date that operations took the asset out of service and made it available for maintenance to make repair.
Step 4 - Determine the TTF or Time to Failure values
This is the time between the first failure date to the next failure date. For example if you experienced a failure on 03/04/1996 and the next failure date was on 5/10/1998 than the TTF value would be 797 days.
5/10/1998 - 03/04/1996 = 797 Days
Step 5 - Determine the Eta and Beta values for the supplied TTF values
The TTF values must be processed utilizing the Weibull calculations to determine the Eta and Beta values. This can be done either manually utilizing a manual method utilizing special Weibull graph paper to more sophisticated tools built especially for performing Weibull analysis. They can also be done to some degree utilizing a generic analytical tool like Microsoft Excel®.
Step 6 - Determine if the data provides a "good fit"
There are several methods to determine the goodness of fit for your analysis results. Common fit tests might include the following:
- Kolmogrov-Smirnov
- R-Squared Values
These tests are beyond the scope of this document.
Step 7 - Determine next steps (PM optimization, Failure Probability, Root Cause Analysis)
The output of a Weibull analysis will help to determine if time base replacement is a suitable strategy for a particular component. It will also help you to determine what the most cost effective time interval should be for wear out failure patterns. In addition to determining the appropriate time based strategy, a Weibull distribution will allow you to determine when a failure might occur so that proper proactive action can be taken to avoid the secondary failure. A common result of a Weibull analysis is to conduct a discipline Root Cause Analysis (RCA). In many cases, the Weibull will indicate that a problem exists that is uncharacteristic for a particular component. An RCA is useful in determining the underlying causes that might be attributing to the poor component performance.
Let's take a look at a practical example. We have a fan that has had several bearing failures. To perform this analysis you have three potential tools to perform your analysis:
- Weibull graph paper (manual)
- Spreadsheet
- Weibull Software
For visual clarity we will use a Weibull software tool to perform our analysis.

Bearing failures on two separate force draft fans (FDF101 and FDF102)

TTF or time to failure values are derived by subtracting the first failure date for an asset from the next subsequent failure date.

The analysis determines that the Beta value is 4.9223, which is indicative of a rapid wear out pattern. In other words, when the bearing begins to first show signs of deterioration, it rapidly progresses to a secondary failure. The Eta value shows that the characteristic life of these bearings are 98.53 days.
The Goodness of Fit test indicates that the data is a good statistical fit for the calculated estimate.
The cumulative distribution Function shows time on the x-axis and probability of failure on the y-axis and in this case it has reliability plotted on the z-axis. To interpret this graph, you can look at any point along the estimate curve and draw a horizontal line to the y-axis and a vertical line to the x-axis to determine the probability of failure at a give time period. You can also see from the graph that this is a wear failure due to the fact that there is no chance of failure until about the 27 day of operation.

The Probability Plot is the plot most often used when conducting a Weibull analysis. It take the data from the Cumulative Distribution Function and plots it onto Log paper to create a straight line. The interpretation is similar to the Cumulative Distribution Function.

Weibull is often used to determine the optimal replacement period for a given component. This is only valid when a wear out pattern exists for the given component (e.g. Beta > 1)
This plot show that if the unplanned repair cost for this component is $10,000 and the planned cost is $3,500 then the recommended replacement interval is 65.94 days.
The Weibull allows the analyst to easily determine when another failure might take place. For instance, if FDF101 and FDF102 are both in service for 24 and 48 days respectively then the likelihood of not surviving another 50 days is 21.59% and 55.70% respectively.
Weibull analysis has been used successfully in a number of industrial applications. It has been particularly useful for helping to determine which turnaround/shutdown to replace heat exchanger bundles. For instance if you have a turnaround/shutdown coming up in 2 months and there will not be another planned outage for 5 years after that then the analyst can review the bundle failure data and run a Weibull analysis to determine if the bundle should be replaced in the upcoming outage or has a high probability of survival for the subsequent planned outage. This has been successfully applied at many refineries with dramatic financial and environmental benefits.

System Reliability Modeling
System Reliability Modeling takes component reliability (e.g. Weibull Analysis) to the next level. For instance, a Weibull can tell you when you can expect to have another component failure on an asset like a fan or a heat exchanger but it cannot tell you how that will affect the system in which that asset resides. That is where system modeling comes into play. System modeling allows the analyst to draw systems with all of the combined assets and asset relationships (e.g. parallel vs series). In addition to defining the physical relationships it also takes into account individual reliability calculations for each asset/component.
To take it one step further, system modeling can also take in financial data to determine what the financial impact would be for a given system failure. This is often done with Monte Carlo simulation. This allows the analyst to simulate many scenarios of a situation to see what the effects would be on a system.
System Modeling Example
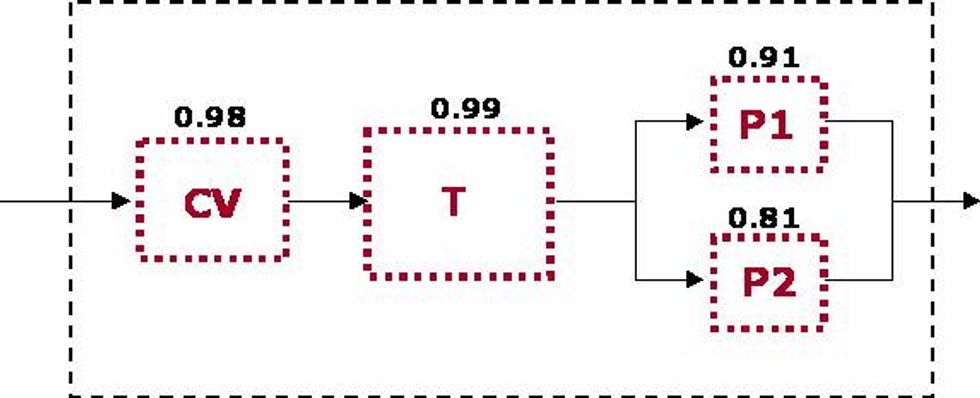
Suppose that you had a control valve, tank and two pumps in the following configuration.

Let's assume that the P2 is full capacity spare for P1 and is only needed when P1 has a failure and cannot perform its function.
The next thing we need to do is determine what the reliability is for each of the assets within the system. In order to determine reliability you will need an accurate MTBF value for each asset. This data can be acquired from plant information systems or from industry standards if plant data does not exist. For simplicity we will use the exponential reliability distribution. This is the equivalent of using the Weibull distribution when Beta is equal to 1.
R(t)=e(-λt)
Let's take a look at the interpretation of this formula.
R(t) - Represents the probability of an asset/component to reach its specified mission time
e - Natural Logarithmic Base (2.718)
λ - 1/MTBF (Lambda)
t - Mission Time
Let's say you have an asset that has a MTBF of 900 days. What would be the
probability of that asset surviving until its specified mission time of 365 days.
R(t) = 2.718 -1/900(365)
R(t) = 2.718 -.4055
R(t) = .6666 or 66.66%
We will now use this calculation as the basis for our system reliability model. Let's build a model of the simple system defined above.

Reliability of series systems is the product of the individual component reliabilities:
Rs = R1 * R2 * ... Rn
Reliability of parallel systems are represented by the following equation:
Rs = 1- (1-R1) * (1-R2) *... (1-Rn)
Let's determine what the reliability of the system is using the specified Reliability values defined in the diagram.
RS = RCV * RT * 1 - [(1-RP1) * (1-RP2)]
RS = 0.98 * 0.99 * 1 - [(1-0.91) * (1-0.81)]
RS = 0.95
This calculation determines that the overall reliability of the system is .95 or 95%. This means that it has a 95% chance that there will be not be a failure that will take the entire system down during the mission time. This is due in large part to the redundancy built into the system on the pump trains. Neither pump train has a reliability value greater than 95% but since they run in parallel we can easily see the increase in system reliability.
As with Weibull Analysis, we have a variety of tools to help us to perform this type of analysis. It can be as simple as doing it by hand or using other software tools like Microsoft Excel® to using very sophisticated tools designed specifically for this type of application.
Case Studies
Marathon Ashland Petroleum
Marathon Ashland Petroleum (MAP), an $8 billion leader in refining, marketing and transportation services uses statistical analysis to determine when a heat exchanger bundle should be replaced. They performed the analysis at the Robinson, IL refinery to determine is the scope on heat exchangers was accurate for their upcoming turnaround.
They performed a series of statistical analyzes and return on investment (ROI) calculations to determine if they should replace bundles in the upcoming turnaround versus the subsequent turnaround. They determined based on the results of the analysis that they should spend an additional $478,490 to replace 26 additional bundles that had a high probability of failure in between the upcoming and subsequent turnarounds. The estimated that they would avoid $2,974,600 in lost profit opportunity by taking the proactive step to replace the bundles instead of taking the increasing risk of failure in between turnarounds.
MAP has now institutionalized the heat exchanger analysis as a corporate best practice and is not performing the analysis at their other 6 refineries across the United States .
ChevronTexaco
ChevronTexaco wanted to investigate the current reliability of their electrical equipment at their Pascagoula MS refinery. The built system reliability models of 13.2 kV Substations to determine what options they had to improve reliability, maintainability, operability with attention give to overall simplicity of the configuration.
The analysis team was able to analyze many different configurations and had the cost benefit for each scenario. The scenarios should the benefit of doing nothing to doing a complete redesign of the system. Sam Preckett, reliability focused maintenance project leader for ChevronTexaco, stated that "ChevronTexaco will be able to avoid approximately $9 million in future lost profit opportunity by using Meridium System Reliability." He went on to say that "now we're preparing to use the product (System Reliability Modeling) for all applicable projects across our enterprise."
Eastman Chemical
Eastman Chemical in Kingsport , TN utilizes a variety of reliability analytics to their chemical operations in Tennessee . They have developed work practices to collect failure event data from the SAP PM maintenance so that they can utilize it for analysis.
Since they have literally 10 of thousands of work orders written every year at their Kingsport complex they needed to devised a method to rank criticality for assets and systems. They are now extremely focused on using sophisticated reliability analytics on their how criticality assets and systems to ensure their reliability and overall performance. They combine the analytical results with data being collected from predictive systems to ensure that they best asset strategy is applied to their critical systems.
Summary
Statistical Reliability methods are very useful and applicable to use in process and manufacturing facilities. The important thing to working with statistics of any kind is to make sure the base data accurately reflects the situation within the facility. There are many training courses on the topic as well as an array of tools and techniques to help get you started. The internet offers an array of educational material to help you begin familiarizing your self with the terminology.
Meridium is a registered trademark of Meridium, Inc., Microsoft Excel is a registered trademark of Microsoft, Inc.
All other trademarks are the property of their respective owners
Learn more at Practical Reliability Group