Asset-intensive enterprises, such as utilities, often face large backlogs of maintenance work orders, which include routine preventive maintenance (PM) tasks and corrective maintenance (CM) actions to address known equipment issues. Since the backlog of work orders usually exceeds the available person-hours on a weekly basis, maintenance supervisors face the ongoing, time-consuming challenge of determining which tasks to prioritize, when to schedule them, and who should be assigned to complete them. This intricate process is like navigating a three-dimensional puzzle that has many more pieces than can fit the available space.
This article highlights a case study in which a mathematical optimization tool was developed and implemented for an electric utility company to automate and optimize the generation of weekly maintenance schedules.
Key Challenges in Scheduling
Maintenance supervisors rely heavily on their domain expertise and experience when making weekly schedules, strategically assigning each worker to complete specific work orders on designated days and times. This raises challenges when these experienced schedulers are out sick or want to retire, introducing a single point of vulnerability and a void in expertise. The volume of open work orders, which for this case study’s utility company can exceed 5,000, with many lingering in the backlog for years, also becomes a mental burden for one person to manage effectively. This, combined with the fact that they may have over 50 workers who each have distinct schedules and skill sets, is a challenge regardless of the scheduler’s expertise. Even if work order prioritization codes are used, it can be difficult to sift through hundreds to thousands of work orders with the same priority level to choose which tasks to do first.
Faced with these challenges, a project was developed to leverage artificial intelligence to automate and improve the maintenance scheduling process. The difficulty in solving this problem was quickly realized, as it was discovered that the schedulers themselves were unable to list all the requirements that go into generating their schedules. Through several rounds of discussions, the following rules that a maintenance schedule must meet became clear:
- Workers can only work during the hours of their scheduled shift. For example, a worker on the day shift (7am-3pm), may only be scheduled during those eight hours. Workers also have time off and training that may affect their availability.
- Each work order has requirements for the number of workers and the number of hours. The workers must be scheduled simultaneously (e.g., one worker cannot be on a four-hour job from 7am-11am, while another is on that same job from 11am-3pm), and they must be scheduled for consecutive hours (e.g., a four-hour job cannot be scheduled in two blocks, say from 9am-11am and then again from 1pm-3pm).
- Some work orders are longer than one shift, stretching across multiple days. These should be scheduled on consecutive days and have some of the same workers on them. For example, if there is a 40-hour work order, it should be scheduled as five eight-hour days from Monday through Friday, and at least one of the workers assigned should be there for all five days for continuity.
- PM work orders have due dates, and they must be completed by their due dates, but not too early. For example, a component may require a PM every six months, but completing the PM six times today does not mean skipping PMs for the next three years. Therefore, it is best to schedule these as close to their due dates as possible.
- Some equipment must be taken out of service to perform maintenance, in which case they have pre-scheduled outage windows that must be created prior to the weekly scheduling process.
- Many work orders require specific skill sets that not every worker has. For example, a work order may require forklift operation or welding. Schedulers must ensure that the workers assigned have the requisite skills for the job, and if they are on a team, an expert can be paired with a novice as part of their training.
Developing a Mathematical Optimization Engine
To automate and optimize this problem, it must be translated into mathematical terms and expressions. This was formulated as a mixed-integer programming (MIP) optimization problem, which is a well-known class of problems with robust commercial and open-source algorithms designed to discover optimal solutions. In fact, these algorithms can guarantee optimality, providing certainty that the solution attained is the best possible.
First, the decision variables were defined. These represent what can be changed while searching for the best schedule. In this case, the decision variables are binary indicators of whether a particular worker is assigned to a particular work order at a particular hour. If a worker is assigned to a job at an hour, the variable corresponding with that worker-job-hour combination is one; otherwise, it is zero. So, for a problem with 3,000 work orders, 50 workers, and eight hours in the day, there are 1,200,000 binary variables. Fortunately, MIP solvers are very efficient and can find optimal solutions for problems at this scale.
Next, a definition is determined for what it means for a solution to be “optimal.” This requires a mathematical objective, which, in this case, is a minimization objective, meaning that the MIP algorithm will manipulate the decision variables to seek the lowest possible value. This objective was formulated in collaboration with the utility company and the schedulers, and it combines the following components into a single score to be minimized:
- PM jobs should be as close to their due dates as possible. The closer they are to the due date, the lower the value.
- Corrective maintenance (CM) jobs should be completed as quickly as possible. The earlier they are completed, the lower the value.
- All jobs (PM and CM) are weighted based on their priority level, the number of hours required, and the number of workers required.
- Penalties are applied for failing to meet certain constraints, such as some of the rules previously described as key challenges. For example, if unable to feasibly schedule a PM job on or before its
- due date, it can be done shortly thereafter, but each day after the due date would increase the objective function value (which the solver is trying to minimize).
- Penalties are applied when workers are available but not assigned to a job. This is sometimes unavoidable, and in those cases, it is often indicative of a need to upskill those workers.
- Penalties are applied when a worker must travel from one location to another in the middle of a shift, as this takes time away from their actual maintenance tasks, sometimes referred to as “wrench time.”
Finally, mathematical constraints were defined to establish what constitutes an acceptable schedule. To comply with the structure of an MIP problem, these are formulated as linear equality or inequality expressions. Meeting the previously stated six rules required 11 additional variables and 26 constraint classes. Each constraint class contains thousands to millions of actual constraints, as some constraint classes get applied to every job and some to every combination of a job, worker and hour.
This problem becomes very large, very fast. With one million decision variables, the number of possible configurations in the schedule is an enormous number that has over 300,000 digits. For this reason, it is impossible to simply list out all the possible configurations and calculate the objective function and whether it violates the constraints. Even if a computer could calculate one trillion configurations per second, this would take an unfathomable number of millennia. Therefore, a code was written that defines the MIP problem, mathematically defining the objective function with all the variables and constraints associated with that specific week’s list of work orders and worker schedules. This MIP problem was sent to a commercial solver that uses an intelligent algorithm to find the best solution, often in minutes.
The workflow for implementing this process is relatively straightforward, as shown in Figure 1. The scheduler initiates the process, and the software takes care of the rest. The software, which already houses work order information, worker shifts and time off schedules, and worker skill sets, sends that information to the optimization engine. Solving the problem typically takes around 10 minutes of computing time. Once it is complete, it generates the proposed optimal work schedule to present to the scheduler. Following the optimization process, the scheduler retains the flexibility to make adjustments before finalizing the schedule. This approach acknowledges the potential for human intervention, recognizing that there may be special considerations or nuanced factors not fully captured in the input data and optimization formulation.
 Figure 1: Workflow for optimization process
Figure 1: Workflow for optimization process
Powering a Better, Faster Scheduling Process
This process was tested on 17 scheduling scenarios that the utility company provided, and the algorithm was able to provide solutions for all of them. Furthermore, the optimization results were 23 percent better than manually generated schedules, as measured by the optimization objective. This process removes the need for subject matter expertise when creating weekly schedules, reduces the amount of time that schedulers need to spend on this weekly task, and ensures the schedule found is a good schedule that doesn’t overlook any work orders or individuals. Since it is integrated into the work planning and scheduling software that houses work order information and personnel details, the process is seamless.
This application of data-driven decision-making can be extended to other companies, scheduling problems, and other routine tasks or decisions. The rapid advances in artificial intelligence (AI) tools and algorithms will make this type of solution more efficient and accessible. The key challenges for companies to adopt this type of solution are:
- They must identify the problems they seek to address;
- They need to develop a precise definition of the problem, objective and rules associated with acceptable and desirable solutions;
- They must ensure their asset information is digitized in a way that is accurate, consistent and continuously updated.
Acknowledgments
This work was done in collaboration with Mr. Anlan Dong, Dr. Amineh Zadbood, and Prof. Lei Wu from Stevens Institute of Technology.






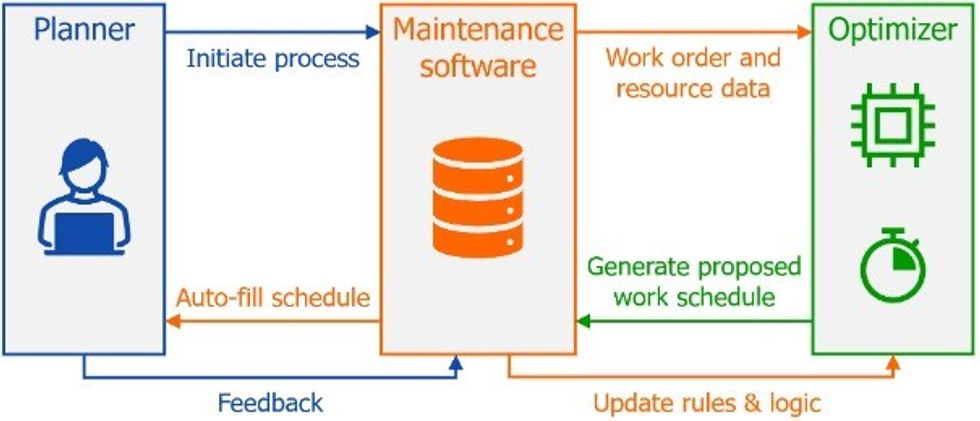 Figure 1: Workflow for optimization process
Figure 1: Workflow for optimization process